Nguyễn Du là Đại thi hào dân tộc, Danh nhân văn hóa thế giới, người đã đưa ngôn ngữ văn học của dân tộc lên một tầm cao mới. Tuy nhiên, không phải ai cũng nắm được cuộc sống và sự nghiệp của ông. Bởi vậy, cùng VUIHOC soạn bài Nguyễn Du – Cuộc đời và sự nghiệp của hai cuốn sách Ngữ Văn 11 Cánh diều và Kết nối tri thức để tìm hiểu về nhà thơ, nhà văn tài ba, xuất chúng này.

1. Soạn bài Tác giả Nguyễn Du - Cuộc đời và sự nghiệp - sách Cánh diều

1.1 Chuẩn bị trước khi đọc văn bản
Tìm hiểu thêm những thông tin về quê hương, gia đình và cuộc đời của Nguyễn Du… Lựa chọn và ghi chép lại một vài thông tin quan trọng có liên quan tới sự nghiệp văn học của tác giả.
Phương pháp giải:
Chú ý lựa chọn những thông tin thật phù hợp, phục vụ cho quá trình đọc hiểu.
Lời giải chi tiết:
* Cuộc đời
- Nguyễn Du sinh năm 1765, mất năm 1820, tự là Tố Như (素如), lấy hiệu Thanh Hiên, biệt hiệu của ông là Hồng Sơn lạp hộ, Nam Hải điếu đồ. Ông là một nhà thơ và nhà văn hóa lớn thời kỳ Lê Mạc, Nguyễn sơ tại Việt Nam. Ông được người dân Việt Nam kính trọng tôn xưng là "Đại thi hào dân tộc" và đã được UNESCO công nhận là "Danh nhân văn hóa thế giới". Ông có một cuộc đời hết sức gian truân và cực khổ.
+ Thuở còn nhỏ Nguyễn Du sống cuộc sống nhung lụa, nhưng cuộc sống ấy kéo dài không quá mười năm. Vì 10 tuổi ông đã mồ côi cha, năm 13 tuổi, lại mồ côi mẹ, ông và các anh em ruột phải sống cùng với người anh cả khác mẹ tên Nguyễn Khản (khi đó ông Khản đã hơn Nguyễn Du những 31 tuổi).
+ Năm 1780 , khi đó Nguyễn Du mới chỉ 15 tuổi thì diễn ra “Vụ mật án Canh Tý”: Chúa Trịnh Sâm lập con thứ là Trịnh Cán lên làm thế tử, thay cho con trưởng của ông là Trịnh Tông. Ông Khản giúp cho Trịnh Tông, nhưng việc bại lộ và bị giam. Đến khi Trịnh Tông lên ngôi, ông Khản đã được cử lên chức Thượng thư Bộ Lại và Tham tụng. Quân lính khác phe (sử sách gọi là “kiêu binh”) không phục, kéo tới phá nhà, khiến ông Khản phải cải trang để trốn lên Sơn Tây sống cùng với em là Nguyễn Điều rồi quay về quê ở Hà Tĩnh. Thế là anh em Nguyễn Du bấy lâu nương tựa ông Khản, mỗi người mỗi ngã.
+ Năm 1783, Nguyễn Du tham gia thi Hương đỗ tam trường (tức tú tài), sau đó không rő vì sao mà không đi thi nữa. Trước kia, một vő quan họ Hà (không rő tên) sống ở Thái Nguyên, không có con nên nhận ông làm con nuôi. Vì thế, khi người cha ấy mất, Nguyễn Du được tập ấm một chức quan vő nho nhỏ ở tỉnh Thái Nguyên.
+ Năm 1802, ông lên nhậm chức Tri huyện ở huyện Phù Dung (nay thuộc Khoái Châu, tỉnh Hưng Yên). Tháng 11 cùng năm, đổi chức thành Tri phủ Thường Tín (Hà Tây, nay thuộc địa phận Hà Nội).
+ Kể từ ấy, Nguyễn Du lần lượt đảm nhận các chức việc sau:
Năm 1803 : tới cửa Nam Quan tiếp sứ thần nhà Thanh của Trung Quốc.
Năm 1805 : được thăng hàm Đông Các điện học sĩ.
Năm 1807 : làm Giám khảo cho trường thi Hương ở tỉnh Hải Dương.
Năm 1809 : làm Cai bạ ở dinh Quảng Bình.
Năm 1813 : thăng Cần Chánh điện học sĩ sau đó giữ chức Chánh sứ đi Trung Quốc.
Sau khi đi sứ trở về vào năm 1814 , ông được thăng lên làm Hữu tham tri Bộ Lễ.
+ Năm 1820, khi Gia Long mất, Minh Mạng (1791-1840) lên ngôi vua, Nguyễn Du lại được cử đi làm Chánh sứ ở Trung Quốc, nhưng chưa kịp lên đường thì ông mất đột ngột (trong một trận dịch vô cùng khủng khiếp làm chết tới hàng vạn người lúc bấy giờ) ở kinh đô Huế vào thời điểm ngày 10 tháng 8 năm Canh Thìn tức là ngày 18 tháng 9 năm 1820. Lúc đầu (năm 1820), Nguyễn Du được an táng ở xã An Ninh thuộc huyện Quảng Điền ở tỉnh Thừa Thiên. Bốn năm sau đó mới cải táng ở Tiên Điền (tỉnh Hà Tĩnh).
- Cuộc đời của Nguyễn Du gắn bó rất sâu sắc với những biến cố trong lịch sử của thời kỳ cuối thế kỉ XVIII – XIX. Đây là giai đoạn lịch sử nhiều biến động với hai đặc điểm nổi bật đó là chế độ phong kiến ở Việt Nam khủng hoảng trầm trọng cùng với phong trào nông dân khởi nghĩa nổi lên ở khắp mọi nơi, đỉnh cao chính là phong trào Tây Sơn.
→ Yếu tố thời đại đã ảnh hưởng rất sâu sắc tới ngòi bút của nhà văn Nguyễn Du khi viết về hiện thực đời sống. Cuộc đời đã từng trải, phiêu bạt nhiều năm ngoài đất Bắc, đi nhiều và tiếp xúc nhiều đã tạo cho Nguyễn Du một vốn sống vô cùng phong phú và niềm thông cảm sâu sắc với những số phận đau khổ của nhân dân. Nguyễn Du là một thiên tài về lĩnh vực văn học và cũng là một nhà nhân đạo chủ nghĩa lớn.
* Sự nghiệp văn học
- Nguyễn Du đã để lại khối di sản văn chương vô cùng đồ sộ với những tác phẩm kiệt xuất, ở thể loại nào thì ông cũng đạt được sự hoàn thiện với trình độ cổ điển. Nguyễn Du là nhà thơ nhân đạo lỗi lạc chất chứa tấm lòng sâu sắc và bao dung, đồng thời ông đã dùng chính ngòi bút ấy để phê phán hiện thực một cách mạnh mẽ, sắc bén.
+ Những tác phẩm viết bằng chữ Hán của Nguyễn Du rất nhiều, nhưng mãi tới năm 1959 mới được ba nhà nho lúc bấy giờ là: Bùi Kỷ, Phan Vő và Nguyễn Khắc Hanh sưu tầm, sau đó phiên dịch, chú thích và giới thiệu lại trong tập: Thơ chữ Hán Nguyễn Du (NXB Văn hóa, 1959) chỉ bao gồm 102 bài. Đến năm 1965 NXB Văn học đã cho ra Thơ chữ Hán Nguyễn Du tập mới do nhà văn, nhà thơ Lê Thước và Trương Chính sưu tầm, chú thích và phiên dịch, sắp xếp, bao gồm 249 bài như: Thanh Hiên thi tập hay còn gọi là Thanh Hiền tiền hậu tập (trong Tập thơ của Thanh Hiên) bao gồm 78 bài thơ ở giai đoạn 1786-1804, nói về 10 năm gió bụi, ông phải sống ở Thái Bình quê vợ, 6 năm trở về nhà dưới chân núi Hồng, và 2 năm làm chi huyện tại huyện Bắc Hà. Tập thơ là những bài viết chủ yếu trong nhiều năm tháng trước khi làm quan nhà họ Nguyễn. Nam trung tạp ngâm (nghĩa là Ngâm nga lặt vặt lúc sống ở miền Nam) bao gồm 40 bài, thời kỳ 1805-1812, ông được thăng hàm Đông các đại học sĩ và làm quan tại Kinh Đô 5 năm và làm cai bạ ở tỉnh Quảng Bình trong vòng 3 năm. Bắc hành tạp lục (tức là Ghi chép linh tinh trong chuyến đi tới phương Bắc) bao gồm 131 bài thơ, thời kỳ 1813-1814, viết trong chuyến đi sứ qua Trung Quốc.
+ Những tác phẩm viết bằng chữ Nôm của tác giả Nguyễn Du bao gồm có: Đoạn trường tân thanh còn có cái tên khác là Kim Vân Kiều truyện bao gồm 3.254 câu thơ viết theo thể lục bát. Văn chiêu hồn (tức Văn tế thập loại chúng sinh có nghĩa là Văn tế mười loại chúng sinh), còn có cái tên khác là Văn chiêu hồn hay Văn tế chiêu hồn.
1.2 Trả lời câu hỏi trong văn bản
Câu 1: Những điểm cần lưu ý về gia đình và dòng họ Nguyễn Du là gì?
Phương pháp giải:
Đọc kĩ đoạn văn thứ hai sau đó tìm những chi tiết về gia đình và dòng họ của Nguyễn Du.
Lời giải chi tiết:
Gia đình, dòng họ Nguyễn Du vừa có truyền thống về khoa bảng và đỗ đạt làm quan vừa có truyền thống về văn hoá và văn học. Họ Nguyễn ở Tiên Điền là dòng họ mang danh vọng lớn đương thời, nhiều người thành đạt trong con đường khoa bảng và công danh.
Câu 2: Những biến cố lịch sử gì đã tác động đến cuộc đời và con người của Nguyễn Du?
Phương pháp giải:
Đọc kĩ đoạn văn thứ bốn sau đó tìm ra những biến cố trong lịch sử và ảnh hưởng đến cuộc đời và con người của Nguyễn Du.
Lời giải chi tiết:
- Những biến cố trong lịch sử đã tác động đến cuộc đời và con người của Nguyễn Du là:
+ Thời kỳ sụp đổ triều đình của vua Lê - chúa Trịnh.
+ Phong trào nông dân khởi nghĩa rầm rộ mà đỉnh cao chính là cuộc khởi nghĩa Tây Sơn.
+ Nguyễn Huệ đã lật đổ vua Lê – chúa Trịnh ở Đàng Ngoài và chúa Nguyễn ở Đàng Trong, đồng thời phá quân Xiêm đã xâm lược tại phương Nam, diệt quân Thanh xâm lược tại phương Bắc đã thu giang sơn lại về một mối và bảo vệ bền vững nền độc lập dân tộc.
+ Triều đại Tây Sơn bị sụp đổ, triều Nguyễn được vua Gia Long (tức Nguyễn Ánh) thiết lập và tiếp đến là công cuộc phồn thịnh trở lại của vương triều họ Nguyễn.
Câu 3: Những điểm đáng lưu ý gì trong cuộc đời của Nguyễn Du có ảnh hưởng đến sáng tác văn chương của ông?
Phương pháp giải:
Đọc kĩ đoạn văn thứ năm sau đó tìm những chi tiết nói về cuộc đời của Nguyễn Du ảnh hưởng tới sáng tác văn chương.
Lời giải chi tiết:
- Nguyễn Du đã sống một cuộc sống đầy thăng trầm: Khi vào cảnh “màn lan trưởng huệ" của cậu công tử trong gia đình đại quý tộc, lúc lại là kẻ phiêu bạt trong cảnh “mười năm gió bụi” lánh nạn ở Tây Sơn; khi là người ẩn cư ở quê nhà, lúc lại làm quan cho triều đình nhà Nguyễn, từng được cử đi làm chánh sứ bên Trung Quốc.
- Đi nhiều và tiếp xúc nhiều cũng là một đặc điểm nổi bật trong cuộc đời của đại thi hào.
+ Bước chân của Nguyễn Du đã từng đi qua nhiều miền quê, từ kinh thành Thăng Long tới kinh đô Huế, từ quê cha ở Hà Tĩnh, quê mẹ ở Bắc Ninh tới quê vợ Thái Bình, rồi lánh nạn tại Thái Nguyên, làm quan tại Quảng Bình,...
+ Những năm tháng đi sứ, Nguyễn Du đi qua nhiều vùng miền trên đất nước Trung Hoa rộng lớn. Ông tiếp xúc và thấu hiểu tất cả tầng lớp người trong xã hội, từ những người hát rong, người ăn xin hay người nông dân tới những người trí thức và quan lại trong triều đình,... Nguyễn Du đã thâu thái được mọi tinh hoa trên những vùng văn hoá lớn của đất nước (Thăng Long, Kinh Bắc, Nghệ – Tĩnh, Huế) và tinh hoa văn hoá ở cả nước ngoài như đất nước Trung Quốc.
→ Sự kết hợp vô cùng hài hòa giữa đời sống với sách vở đã tạo nên một đại thi hào của dân tộc là Nguyễn Du.

Câu 4: Chú ý vào những tác phẩm tiêu biểu của nhà văn Nguyễn Du.
Phương pháp giải:
Đọc kĩ đoạn văn thứ hai của phần II sau đó tìm ra những tác phẩm tiêu biểu.
Lời giải chi tiết:
- Những tác phẩm văn học tiêu biểu của Nguyễn Du:
+ Thơ chữ Hán, Nguyễn Du sở hữu 3 tập thơ (Nam trung tạp ngâm, Thanh Hiên thi tập, Bắc hành tạp lục).
+ Thơ chữ Nôm, Nguyễn Du sở hữu hai kiệt tác là “Truyện Kiều” và tác phẩm “Văn tế thập loại chúng sinh”.
Câu 5: Chú ý về hiện thực xã hội được phản ánh ở những sáng tác của Nguyễn Du.
Phương pháp giải:
Đọc kĩ phần 1 sau đó chú ý đến hiện thực xã hội
Lời giải chi tiết:
Hiện thực xã hội được phản ánh ở những sáng tác của Nguyễn Du: tái hiện về hoàn cảnh sống của những cuộc đời cơ cực và hẩm hiu (ông già mù đi hát rong, người mẹ dắt theo con đi ăn xin,…), những con người với sắc tài xuất chúng mà lại bi kịch (người phụ nữ gảy đàn ở đất Long Thành hay nàng Tiểu Thanh;…).
Đó là những bất công trong xã hội, những cảnh đời vô cùng trái ngược.
Câu 6: Tấm lòng nhân đạo của nhà văn Nguyễn Du được thể hiện như thế nào thông qua thơ chữ Hán?
Phương pháp giải:
Đọc kĩ đoạn văn thứ ba trong phần II sau đó tìm ra tấm lòng nhân đạo của nhà văn Nguyễn Du.
Lời giải chi tiết:
Thơ chữ Hán của Nguyễn Du như cuốn nhật ký cuộc đời của tác giả, là bức chân dung tự vẽ về một con người với tấm lòng nhân đạo sâu sắc, bao la, thương người và cũng tự thương mình:
+ Nguyễn Du hướng tới những số phận vô cùng đau khổ và bất hạnh với niềm cảm thương hết sức sâu sắc. Đó là những người phụ nữ có sắc tài mà lại bạc mệnh, đó là những người nghèo khổ mà tác giả đã bắt gặp trên đường đi sứ.
+ Viết về những con người sở hữu tài năng, có khi tiết thanh cao, Nguyễn Du vừa thể hiện lên niềm cảm thương, lại vừa trân trọng và ngưỡng mộ. Nguyễn Du cảm thấy mình là một người cùng hội cùng thuyền với những cuộc đời tài năng mà bị kịch ấy.
+ Do đó, từ lòng thương người, Nguyễn Du đã trở lại với niềm tự thương. Tự thương cũng là tự có ý thức với cá nhân. Niềm tự thương chính là một nét mới trong tinh thần nhân đạo của nhà văn Nguyễn Du.
Câu 7: Chú ý vào những nội dung hình thành nên giá trị nhân đạo của tác phẩm Truyện Kiều.
Phương pháp giải:
Đọc kĩ đoạn văn thứ năm và sáu trong phần II sau đó tìm ra nội dung của Truyện Kiều đã thể hiện rő nét giá trị nhân đạo.
Lời giải chi tiết:
- Những nội dung:
+ Tiếng nói vô cùng đồng cảm trước số phận cay nghiệt của con người trong tác phẩm Truyện Kiều thể hiện tập trung thông qua hình tượng nhân vật Thúy Kiều. Nhân vật phải chịu một cuộc sống hội tụ đầy đủ những khốn khổ của con người nói chung và người phụ nữ nói riêng: tình yêu, gia đình cho tới nhân phẩm,…
+ Tiếng nói đồng tình với những khát vọng chân chính của con người được thể hiện tập trung thông qua tình yêu của Kim Trọng với nhân vật Thúy Kiều, tình yêu Kim – Kiều đã tan vỡ nhưng khát vọng về tình yêu không mất đi. Trải qua biết bao nhiêu đau khổ nhưng Thúy Kiều vẫn muốn vươn lên tới những khát vọng mạnh mẽ. Sau đó khi gặp được Từ Hải, đây là một hiện thân của khát vọng tự do và công lí.
→ Viết Truyện Kiều, Nguyễn Du đã thể hiện lên tiếng nói đồng cảm với những bi kịch, đồng tình với những khát vọng hết sức chân chính của con người. Đó cũng chính là giá trị nhân đạo mà kiệt tác văn chương này muốn thể hiện.
Câu 8: Điểm nổi bật trong thơ chữ Hán của Nguyễn Du là gì?
Phương pháp giải:
Đọc kĩ đoạn văn thứ chín trong phần II sau đó tìm ra điểm nổi bật của thơ chữ Hán.
Lời giải chi tiết:
Thơ chữ Hán của Nguyễn Du là những áng văn chương vô cùng tuyệt tác, phần lớn được viết bằng thể thơ Đường luật với đủ những tiểu loại: nếu xét tới số câu trong bài thì có tứ tuyệt (hay tuyệt cú), bát cú và trường thiên; nếu xét tới số chữ trong câu thì có các loại ngũ ngôn, lục ngôn và thất ngôn. Bút pháp nghệ thuật rất phong phú và đa dạng: tự sự hiện thực, trữ tình và trào phúng. Tính chất mang sự hàm súc và cô đọng, “ý tại ngôn ngoại” (nghĩa là ý ở ngoài lời), nghệ thuật đối,... vốn là những đặc điểm và thế mạnh ở thơ Đường luật được nhà thơ phát huy ở mức mạnh mẽ nhất. Chất trữ tình hoà lẫn chất triết lí đem tới sự thâm trầm và sâu sắc trong thơ chữ Hán của Nguyễn Du.
Câu 9: Chú ý tới những thành công trong nghệ thuật lớn của tác phẩm Truyện Kiều.
Phương pháp giải:
Đọc kĩ đoạn văn mười một trong phần II sau đó tìm ra những nghệ thuật đặc sắc trong tác phẩm Truyện Kiều.
Lời giải chi tiết:
- Nghệ thuật:
+ Chuyển thể từ tiểu thuyết chương hồi qua truyện thơ Nôm vì vậy đã kết hợp được thế mạnh giữa cả tự sự (là yếu tố truyện) và trữ tình (là yếu tố thơ).
+ Điểm nhìn trần thuật từ người bên ngoài câu chuyện thành người trong cuộc.
+ Cốt truyện rất sáng tạo, kết thúc về hình thức chính là có hậu nhưng bản chất lại là bi kịch.
+ Xây dựng nhân vật: Phân loại tốt – xấu rő ràng như truyện cổ tích nhưng cũng có những nhân vật không thể phân loại tốt – xấu đan xen.
+ Xây dựng nội tâm nhân vật bằng những bút pháp ước lệ và tả thực có ý nghĩa cách tân.
+ Những câu thơ lục bát vừa mang vẻ dân dã bình dị lại vừa mang nét trau chuốt nghệ thuật và đạt đến giá trị khuôn thước chuẩn mực.
+ Kết hợp ngôn ngữ trong đời sống, ngôn ngữ trong văn học dân gian với ngôn ngữ của bác học kết tinh từ sách vở.
1.3 Trả lời câu hỏi sau khi đọc văn bản
Câu 1 trang 43 SGK Văn 11/1 Cánh diều
Văn bản Nguyễn Du - Cuộc đời và sự nghiệp được chia thành mấy phần? Hãy xác định những nội dung chính của mỗi phần.
Phương pháp giải:
Đọc kĩ toàn bài sau đó dựa vào nội dung các phần để xác định được bố cục.
Lời giải chi tiết:
- Văn bản Nguyễn Du - Cuộc đời và sự nghiệp được chia làm 2 phần chính:
+ Phần 1: Cuộc đời đã từng trải với vốn sống vô cùng phong phú của Nguyễn Du.
+ Phần 2: Sự nghiệp văn chương của Đại thi hào Nguyễn Du.
Câu 2 trang 43 SGK Văn 11/1 Cánh diều
Dựa vào văn bản phía trên, em hãy nêu ra những điểm nổi bật liên quan đến thời đại, gia đình và cuộc đời của Nguyễn Du có ảnh hưởng đến sáng tác của ông.
Phương pháp giải:
Đọc lại toàn bộ bài, chú ý tới những chi tiết thời đại, gia đình và cuộc đời có ảnh hưởng tới sáng tác của ông.
Lời giải chi tiết:
- Gia đình: Nguyễn Du được sinh trưởng trong một gia đình đại quý tộc, nhà ông có nhiều đời làm quan và có truyền thống về khía cạnh văn học. Cha là Nguyễn Nghiễm, thi đỗ tiến sĩ, từng giữ chức vị Tể tướng. Chính điều đó là cái nôi nuôi dưỡng lên tài năng văn học của ông.
- Thời đại: Cuộc đời của Nguyễn Du gắn liền với những biến cố trong lịch sử của thời kỳ cuối thế kỉ XVIII – XIX. Đây chính là giai đoạn lịch sử với đầy những biến động, có hai đặc điểm nổi bật chính là chế độ phong kiến ở Việt Nam bị khủng hoảng trầm trọng và phong trào nông dân khởi nghĩa nổ ra rầm rộ khắp mọi nơi, đỉnh cao chính là phong trào Tây Sơn. Yếu tố thời đại đã ảnh hưởng vô cùng sâu sắc đến ngòi bút của Nguyễn Du khi viết về hiện thực của đời sống.
Câu 3 trang 43 SGK Văn 11/1 Cánh diều
Vì sao bài viết lại khẳng định thơ chữ Hán của Nguyễn Du “là bức chân dung tự hoạ về một con người có tấm lòng nhân đạo bao la, sâu sắc"?
Phương pháp giải:
Tìm lại phần nội dung trong thơ chữ Hán và sau đó đưa ra những bình luận phân tích của bài viết đưa ra về ý kiến phía trên.
Lời giải chi tiết:
Bài viết đã khẳng định thơ chữ Hán của Nguyễn Du “là bức chân dung tự hoạ về một con người có tấm lòng nhân đạo bao la, sâu sắc" do nét nổi bật chính trong những sáng tác của Nguyễn Du là về sự đề cao xúc cảm, nghĩa là đề cao “tình”. Điều quan trọng nhất, là sự cảm thông vô cùng sâu sắc của tác giả đối với cuộc sống và đối với con người, đặc biệt là những con người nhỏ bé và bất hạnh.
Câu 4 trang 43 SGK Văn 11/1 Cánh diều
Giá trị nhân đạo của tác phẩm Truyện Kiều thể hiện ở những khía cạnh nào? Điểm tương đồng và điểm khác biệt về nội dung nhân đạo giữa tác phẩm Truyện Kiều với thơ chữ Hán của Nguyễn Du là gì?
Phương pháp giải:
Đọc lại phần mang giá trị nhân đạo của tác phẩm Truyện Kiều, chỉ ra thể hiện ở những khía cạnh nào. Tìm ra nội dung nhân đạo trong thơ chữ Hán Nguyễn Du sau đó so sánh chỉ ra điểm khác biệt.
Lời giải chi tiết:
- Giá trị nhân đạo trong Truyện Kiều được thể hiện ở:
+ Cảm hứng chủ đạo của tác giả Nguyễn Du khi viết Truyện Kiều chính là nỗi đau đứt ruột từ “những điều trông thấy”, như chính nhan đề của tác phẩm là Đoạn trường tân thanh (tức Tiếng kêu mới về nỗi đau tới đứt ruột gan).
+ Cốt truyện của tác phẩm Truyện Kiều giống với nhiều truyện Nôm có ba phần là Gặp gỡ – Thử thách — Đoàn tụ nhưng đồng thời cũng có những sáng tạo mới khi tác giả đã xây dựng một kết thúc về mặt hình thức là có hậu nhưng bản chất lại là bi kịch.
+ Truyện Kiều có những tuyến nhân vật, phân theo loại tốt – xấu, thiện – ác rő ràng, giống kiểu nhân vật trong truyện cổ tích, nhưng cũng có những nhân vật không thể phân loại được, khi tốt – xấu đan xen. Những nhân vật trong tác phẩm Truyện Kiều là những nhân vật có tính cách, hơn nữa tính cách lại có sự thay đổi bởi những tác động của hoàn cảnh như với nhân vật Thuý Kiều. Tính cách nhân vật đã được khắc họa thông qua cả bút pháp ước lệ lẫn bút pháp tả thực, bằng con người với biểu hiện ở bên ngoài và cả con người với đời sống nội tâm.
+ Miêu tả nội tâm của nhân vật là một thành công nghệ thuật rất lớn, mang ý nghĩa cách tân cho kiệt tác Truyện Kiều. Thiên nhiên trong Truyện Kiều vừa là đối tượng thẩm mĩ lại vừa là phương thức để thể hiện tâm trạng của nhân vật sử dụng nghệ thuật "tả cảnh ngụ tình".
- Khác biệt: Trong Truyện Kiều, tính cách của nhân vật được khắc họa thông qua cả bút pháp ước lệ lẫn bút pháp tả thực, bằng con người với biểu hiện ở bên ngoài và cả con người với đời sống nội tâm, nó có ý nghĩa cách tân cho kiệt tác Truyện Kiều. Còn trong thơ chữ Hán của nhà văn Nguyễn Du thì lại không có điều này.
Câu 5 trang 43 SGK Văn 11/1 Cánh diều
Truyện Kiều sở hữu những thành công nào về nghệ thuật?
Phương pháp giải:
Tìm ra những nghệ thuật đặc sắc trong Truyện Kiều đã được chỉ ra trong bài.
Lời giải chi tiết:
- Nghệ thuật:
+ Chuyển thể từ tiểu thuyết chương hồi qua truyện thơ Nôm do đó đã kết hợp được thế mạnh về cả tự sự (là yếu tố truyện) và trữ tình (là yếu tố thơ).
+ Điểm nhìn trần thuật từ người đứng ngoài câu chuyện thành người trong cuộc.
+ Cốt truyện sáng tạo, kết thúc về hình thức là có hậu nhưng bản chất là bi kịch.
+ Xây dựng nhân vật: Phân loại rő ràng tốt – xấu như trong truyện cổ tích nhưng cũng có nhân vật không phân loại được, tốt – xấu đan xen.
+ Xây dựng nội tâm nhân vật bằng những bút pháp ước lệ với tả thực mang tới ý nghĩa cách tân.
+ Những câu thơ lục bát vừa có nét dân dã bình dị lại vừa có nét trau chuốt về nghệ thuật, đạt đến giá trị khuôn thước của chuẩn mực.
+ Kết hợp giữa ngôn ngữ đời sống, ngôn ngữ văn học dân gian cùng với ngôn ngữ bác học kết tinh qua sách vở.
Câu 6 trang 43 SGK Văn 11/1 Cánh diều
Nhà thơ Tố Hữu đã nhận định rằng Nguyễn Du là “người xưa của ta nay”. Em có suy nghĩ như thế nào về nhận định đó?
Phương pháp giải:
Trình bày suy nghĩ dựa vào việc giải thích nhận định và phân tích, bình luận nhằm làm rő.
Lời giải chi tiết:
Nguyễn Du là một đại thi hào của toàn dân tộc Việt Nam. Những tác phẩm của ông chất chứa những giá trị về tư tưởng, triết lí sống rất sâu sắc, cũng bởi vậy mà Tố Hữu đã nhận định về ông là “người xưa của ta nay”. “Người xưa” là muốn nhắc tới Nguyễn Du với những mong ước và khát khao lớn lao, còn “ta nay” chính là muốn nói tới Tố Hữu cũng có những suy nghĩ và khát khao như Nguyễn Du. Trong nhiều sáng tác của ông cũng đề cao tới giá trị nhân văn của con người. Những tác phẩm ấy đều thể hiện về sự cảm thông sâu sắc của Nguyễn Du đối với cuộc đời của con người, nhất là với những người nhỏ bé và bất hạnh, ... đó là kết quả của cả một quá trình quan sát và suy ngẫm về cuộc đời, con người của nhà văn. Qua kiệt tác Truyện Kiều của Nguyễn Du, ông đã ca ngợi và đề cao hình ảnh của người phụ nữ vừa xinh đẹp, tài hoa nhưng lại bạc mệnh. Ông sẵn sàng lên án và tố cáo những thế lực đen tối đã chà đạp lên con người. Ông đề cao về quyền bình đẳng và giá trị của mỗi con người. Tư tưởng của nhà văn Nguyễn Du đã vượt qua thời đại để có thể tồn tại đến bây giờ.
2. Soạn bài Tác giả Nguyễn Du - Cuộc đời và sự nghiệp - sách Kết nối tri thức
2.1 Trả lời câu hỏi trước khi đọc văn bản
Truyện Kiều của tác giả Nguyễn Du đã hòa nhập vào đến đời sống và sinh hoạt văn hóa của dân tộc Việt Nam. Bạn hãy nêu ra một trường hợp có sử dụng các hình thức đố Kiều, lẩy Kiều hoặc vịnh Kiều.
Lời giải chi tiết:
Kể từ khi Truyện Kiều được phổ biến một cách rộng rãi cho đến ngày nay, thiên hạ vẫn tiếp tục tìm kiếm sức hấp dẫn và nghiên cứu kiệt tác này dưới các góc độ khác nhau. Có lẽ, trên thế giới chỉ có duy nhất Truyện Kiều là trường hợp mà độc giả đã sử dụng tác phẩm để bói cho số phận của mình. Và bản thân tác phẩm cũng đã được quần chúng sử dụng để trở thành một sinh hoạt văn hóa vô cùng đa dạng. Ta có thể kể tới: tập Kiều, lẩy Kiều, bói Kiều, đố Kiều, vịnh Kiều, nhại Kiều,…
Ví dụ về một hình thức đố Kiều như sau:
Đố:
“Truyện Kiều” anh đã thuộc làu
Đố anh kể được một câu năm người?
Giải:
Này chồng, này mẹ, này cha
Này là em ruột, này là em dâu!
- Bài Vịnh Kiều (của tác giả Đỗ Như Tâm):
“Sắc tài có một đỉnh đình đinh,
Khắp cả giang sơn tiếng nổi phình.
Duyên chị mà em theo lẽo đẽo,
Nợ chàng rồi thiếp sạch sành sanh.
Ra đi đầu đội muôn phần hiếu,
Trở lại vai mang một chữ tình.
Mười mấy năm trời nhớ rửa sạch,
Khúc đờn nhàn khảy tính tình tinh.”
- “Lẩy Kiều” có thể hiểu là sự lựa chọn những câu thích hợp trong số 3.254 câu của Truyện Kiều sau đó nối lại sao cho có vần và có nghĩa theo đúng dụng ý riêng của mình, để tạo ra một bài viết nói về một chuyện nào đó. Ví dụ trong đoạn “nói chuyện tại cuộc mít tinh chào mừng Tổng thống Xu-các-nô” thuộc nước Cộng hòa In-đô-nê-xi-a năm 1959. Người có nói:
“Nước xa mà lòng không xa
Thật là bầu bạn, thật là anh em.”

2.2 Trả lời câu hỏi trong khi đọc văn bản
Câu 1: Truyền thống gia đình, dòng họ cũng như bối cảnh thời đại Nguyễn Du
Lời giải chi tiết:
Sinh ra trong gia đình đại quý tộc, nhiều đời nhà ông làm quan và có truyền thống trong lĩnh vực văn học: cha là Nguyễn Nghiễm, đã đỗ tiến sĩ, từng giữ chức vị Tể tướng; anh cùng cha khác mẹ của ông là Nguyễn Khản từng làm quan lớn dưới triều Lê - Trịnh. Nhưng sớm mồ côi cả cha lẫn mẹ (mồ côi cha từ năm lên 10 tuổi, mồ côi mẹ khi mới 12 tuổi). Hoàn cảnh gia đình cũng có tác động to lớn đến sáng tác của Nguyễn Du.
Thời đại:
Cuộc đời của Nguyễn Du gắn bó sâu sắc với nhiều biến cố lịch sử của thời kỳ cuối thế kỉ XVIII và đầu thế kỉ XIX. Những tập đoàn phong kiến Lê - Trịnh - Nguyễn đang tranh giành quyền lực
Chế độ phong kiến ở Việt Nam khủng hoảng một cách trầm trọng, xã hội rối ren và cuộc sống của nhân dân rơi vào cảnh cơ cực, lầm than.
Phong trào khởi nghĩa nổ ra khắp nơi, tiêu biểu nhất chính là cuộc khởi nghĩa Tây Sơn do Quang Trung (hay Nguyễn Huệ) lãnh đạo.
Nghĩa quân Tây Sơn đã đánh đổ được tập đoàn phong kiến Trịnh, Lê và Nguyễn, quét sạch hai mươi vạn quân xâm lược của nhà Thanh đưa sang xâm lược.
Câu 2: Những dấu mốc quan trọng trong cuộc đời của Nguyễn Du.
Lời giải chi tiết:
Cuộc đời của Nguyễn Du gắn bó sâu sắc với nhiều biến cố lịch sử trong giai đoạn cuối thế kỉ XVIII – XIX. Yếu tố thời đại đã ảnh hưởng vô cùng sâu sắc tới ngòi bút của nhà văn Nguyễn Du khi viết về hiện thực của đời sống. Cuộc đời từng trải và phải phiêu bạt nhiều năm trên đất Bắc, được đi nhiều và tiếp xúc nhiều đã tạo cho Nguyễn Du một vốn sống phong phú và niềm thông cảm rất sâu sắc với những số phận đau khổ của nhân dân. Nguyễn Du là một thiên tài về văn học và là một nhà nhân đạo chủ nghĩa lớn.
Thuở nhỏ Nguyễn Du được sống trong nhung lụa, nhưng cuộc sống đó kéo dài không quá mười năm. Vì 10 tuổi đã mồ côi cha, và năm 13 tuổi ông lại mồ côi mẹ, ông và những anh em ruột phải tới sống với người anh cả khác mẹ tên là Nguyễn Khản (khi ấy ông Khản hơn Nguyễn Du những 31 tuổi).
Năm 1780 , khi đó Nguyễn Du mới chỉ 15 tuổi thì xảy ra “Vụ mật án Canh Tý”: Chúa Trịnh Sâm lập đứa con thứ là Trịnh Cán lên làm thế tử, thay cho con trưởng của ông là Trịnh Tông. Ông Khản đã giúp Trịnh Tông, việc bị bại lộ và bị giam.
Năm 1783, Nguyễn Du đã thi Hương đỗ tam trường (tức tú tài), sau đó không rő vì sao mà không đi thi nữa. Trước đây, một vő quan họ Hà (không biết rő tên) tại Thái Nguyên, không có con nên đã từng nhận ông làm con nuôi. Vì vậy, khi người cha ấy mất, Nguyễn Du đã được tập ấm một chức quan vő nho nhỏ tại Thái Nguyên.
Năm 1802, ông lên nhậm chức Tri huyện tại huyện Phù Dung (nay thuộc Khoái Châu, tỉnh Hưng Yên ). Tháng 11 cùng năm, đổi lên làm Tri phủ Thường Tín (Hà Tây, nay thuộc địa phận Hà Nội).
Kể từ ấy, Nguyễn Du lần lượt đảm đương các chức việc sau:
+ Kể từ ấy, Nguyễn Du lần lượt đảm nhận các chức việc sau:
Năm 1803 : tới cửa Nam Quan tiếp sứ thần nhà Thanh của Trung Quốc.
Năm 1805 : được thăng hàm Đông Các điện học sĩ.
Năm 1807 : làm Giám khảo cho trường thi Hương ở tỉnh Hải Dương.
Năm 1809 : làm Cai bạ ở dinh Quảng Bình.
Năm 1813 : thăng Cần Chánh điện học sĩ sau đó giữ chức Chánh sứ đi Trung Quốc.
Sau khi đi sứ trở về vào năm 1814 , ông được thăng lên làm Hữu tham tri Bộ Lễ.
+ Năm 1820, khi Gia Long mất, Minh Mạng (1791-1840) lên ngôi vua, Nguyễn Du lại được cử đi làm Chánh sứ ở Trung Quốc, nhưng chưa kịp lên đường thì ông mất đột ngột (trong một trận dịch vô cùng khủng khiếp làm chết tới hàng vạn người lúc bấy giờ) ở kinh đô Huế vào thời điểm ngày 10 tháng 8 năm Canh Thìn tức là ngày 18 tháng 9 năm 1820. Lúc đầu (năm 1820), Nguyễn Du được an táng ở xã An Ninh thuộc huyện Quảng Điền ở tỉnh Thừa Thiên. Bốn năm sau đó mới cải táng ở Tiên Điền (tỉnh Hà Tĩnh).

Câu 3:Chú ý vào hoàn cảnh sáng tác, nội dung cơ bản cùng với đặc sắc trong nghệ thuật của từng tập thơ Thanh Hiên thi tập, Nam trung tạp ngâm và Bắc hành tạp lục.
Lời giải chi tiết:
a. Thanh Hiên thi tập:
- Hoàn cảnh ra đời: viết vào những năm trước 1802, để nói về tình cảnh và tâm sự của mình trong cuộc sống lênh đênh, lưu lạc hoặc trong thời gian đang ẩn náu tại quê nhà, lúc gia đình ông sa sút theo đà sụp đổ của chế độ nhà Lê - Trịnh.
- Nội dung: chứa đựng những tình cảm về quê hương thân thuộc, có khi ốm đau mà chẳng cần thuốc thang gì, có lúc đói rét phải nhờ vả vào lòng thương của người khác. Tâm sự của tác giả vào thời điểm này là một tâm sự vô cùng buồn rầu, có khi chán nản và uất ức… Thanh Hiên thi tập ghi lại những tâm sự của một con người đầy hùng tâm và tráng chí nhưng gặp những cảnh ngộ không như ý cho nên phải ôm trong lòng nỗi u uất không thể giải tỏa. Bao trùm tập thơ là những điệp khúc buồn và u uẩn đến day dứt khôn nguôi.
- Nghệ thuật: thơ chữ Hán có sử dụng nhiều điển tích, điển cố.
b. Nam trung tạp ngâm:
- Hoàn cảnh ra đời: gồm những bài thơ sáng tác từ năm 1805 đến cuối năm 1812, tức là từ khi ông được thăng hàm Đông các điện học sĩ ở Huế cho tới hết thời kỳ làm Cai bạ dinh Quảng Bình. Tập thơ bao gồm 40 bài, mở đầu tập là bài Phượng hoàng lộ thượng tảo hành (tức là Trên đường Phượng Hoàng) và cuối tập là bài Đại tác cửu tư quy (tức là Làm thay người đi thú lâu năm mong về).
- Nội dung: nói lên sự nghèo túng và ốm đau của mình (Ngẫu đề, Thủy Liên đạo trung tảo hành...) hay nói một cách khác mỉa mai và bóng gió hơn về thói hay chèn ép của bậc quan lại (Ngẫu đắc, Điệu khuyển...).
- Nghệ thuật: giọng điệu vô cùng bi thiết và buồn thương. Còn về phong cách, thơ Nguyễn Du chứa giọng nhu, khoan thai mà lại tha thiết lắng sâu và hết mực chân thành, cảm hứng trữ tình cùng với cảm hứng hiện thực được đan xen tạo ra tính chất vừa thống nhất lại vừa phân hóa tương đối của cảm hứng nghệ thuật nói chung trong thơ chữ Hán của Nguyễn Du. Trong đó, cảm hứng trữ tình vẫn luôn chiếm ưu thế hơn hết và tạo ra âm hưởng chủ đạo cho hai tập thơ. Đó là thế giới tinh thần chứa đầy u uất, buồn thương cùng những vận động nội tâm vô cùng sâu sắc của một con người luôn khao khát được sống nhưng thời thế lắm điều không như ý.
c. Bắc hành tạp lục:
- Hoàn cảnh ra đời: sáng tác vào thời gian ông đi sứ Trung Quốc
- Nội dung: là nỗi cảm thương trăn trở và day dứt trước số phận của con người, đặc biệt là những người tài hoa. Với đề tài hiện thực, Nguyễn Du từ cői lòng chứa đầy những thất vọng khổ đau của riêng mình đề cập tới những trăn trở trước số phận của con người. Xuất hiện trong tập thơ là hiện thực của những nhân dân cùng khổ, Nguyễn Du đã vẽ nên những bức tranh hết sức sống động về tình cảnh của những người dân nghèo trong bước đường tha phương.
- Nghệ thuật: thơ chữ Hán có sử dụng các cặp thơ đối.
Câu 4: Giá trị chung trong thơ chữ Hán của Nguyễn Du
Lời giải chi tiết:
Nguyễn Du đã vượt qua những ràng buộc của ý thức hệ phong kiến và tôn giáo để có thể vươn lên khẳng định được giá trị tự thân của con người. Thơ ông, nhất là thơ chữ Hán luôn bộc lộ sự trân trọng, ca ngợi lên vẻ đẹp, khát vọng sống và khát vọng tình yêu, được hạnh phúc. Với gia tài thơ chữ Hán của mình, Nguyễn Du đã góp phần to lớn trong việc làm nên những thành tựu của một thời kỳ rực rỡ nhất trong lịch sử của văn học dân tộc.
Thơ chữ Hán của Nguyễn Du vừa lưu giữ được thế giới tâm hồn phong phú và phức tạp của một nghệ sĩ lớn, vừa có thể khái quát hiện thực rất cao và mang tới giá trị nhân văn vô cùng sâu sắc.
Câu 5: Lưu ý về mối liên hệ giữa hai văn bản: Truyện Kiều (tác giả Nguyễn Du) và Kim Vân Kiều truyện (tác giả Thanh Tâm Tài Nhân).
Lời giải chi tiết:
Truyện Kiều được viết dựa trên hình thức truyện thơ Nôm, viết bằng thể lục bát, gồm 3254 câu, kể về cuộc đời mười lăm năm sống chìm nổi của Thuý Kiều. Sáng tác Truyện Kiều, Nguyễn Du đã tiếp thu đề tài và cốt truyện từ Kim Vân Kiều truyện của tác giả Thanh Tâm Tài Nhân (tác giả Trung Quốc). Việc kế thừa cốt truyện của tác giả đi trước là một biểu hiện của quá trình giao lưu văn hoá, xuất hiện trong nhiều nền văn học Trung đại trên toàn thế giới.
Câu 6: Chú ý về nội dung cơ bản của tư tưởng nhân đạo trong tác phẩm Truyện Kiều.
Lời giải chi tiết:
Truyện Kiều chứa đựng nhiều tư tưởng nhân đạo lớn lao, sâu sắc và độc đáo. Tư tưởng ấy trước hết được bộc lộ quá cảm hứng tôn vinh lên vẻ đẹp của con người, đặc biệt là những người phụ nữ. Nguyễn Du thuộc số ít những tác giả thời trung đại quan tâm và trân trọng con người một cách toàn diện, cả tâm hồn lẫn thể xác.
* Phê phán về xã hội bất công, tàn ác và luôn chèn ép con người
– Vạch trần bộ mặt xấu xa của lũ quan lại, những kẻ chỉ biết “buôn thịt bán người”, kiếm tiền trên thân xác của những người con gái.
– Lên án xã hội đồng tiền đã chà đạp lên phẩm giá và hạnh phúc của con người.
=> Ngòi bút tả thực của tác giả Nguyễn Du đã phơi bày ra bộ mặt thật của xã hội phong kiến thối nát bấy giờ, trong đó đồng tiền có thể xoay chuyển mọi thứ, thao túng con người và dung túng cho tội ác.
* Ca ngợi và thêm trân trọng những vẻ đẹp của con người
– Khắc họa rất sống động vẻ đẹp về ngoại hình của chị em Thúy Kiều, lấy thiên nhiên làm thước đo cho vẻ đẹp của con người.
– Ca ngợi và trân trọng vẻ đẹp tâm hồn: Thúy Vân thì thanh cao và đài các, Thúy Kiều thì sắc sảo và mặn mà.
– Ca ngợi lên tài năng của Thúy Kiều đó là: cầm kỳ thi họa đều rất tinh thông
* Đồng cảm và xót thương với những số phận bất hạnh:
– Xót thương cho những kiếp người tài hoa mà bạc mệnh
– Thương cho những con người bị chà đạp, ức hiếp và bị biến thành món hàng mặc cho người ta mua bán.
Câu 7: Khát vọng về tình yêu và khát vọng về tự do
Lời giải chi tiết:
Yêu thương, trân trọng con người cho nên Nguyễn Du mới đồng cảm và đồng tình với những khát vọng chính đáng, vượt lên một số khuôn phép phản nhân văn trong tư tưởng phong kiến. Đó là khát vọng về tình yêu tự do được khẳng định thông qua mối tình Kim - Kiều trong sáng, thuỷ chung và cao thượng. Ngòi bút đậm chất trữ tình của tác giả Nguyễn Du đã mở ra cả một thế giới mới vừa phong phú, lại bí ẩn của trái tim đang yêu với đủ những cung bậc cảm xúc khác nhau; mang tới cái nhìn mới mẻ và sâu sắc trong tình yêu. Nguyễn Du vẫn vô cùng trân trọng tình yêu mà Thúy Kiều dành cho Kim Trọng, Thúc Sinh hay Từ Hải. Đó còn chính là khát vọng được sống tự do mà Nguyễn Du thể hiện thông qua nhân vật Từ Hải, giấc mơ công lí đã được chuyển tải thông qua phiên tòa báo ân báo oán.
Câu 8: Mô hình về cốt truyện của tác phẩm Truyện Kiều
Lời giải chi tiết:
Cốt truyện của Truyện Kiều đã được xây dựng theo mô hình chung của những truyện thơ Nôm với ba phần chính là Gặp gỡ - Chia ly - Đoàn tụ. Trong mỗi phần, Nguyễn Du đều có những sáng tạo vô cùng độc đáo. Chẳng hạn, đoạn kết của Truyện Kiều không viên mãn như những truyện thơ Nôm khác vì sau cuộc đoàn tụ, tuyến nhân vật chính đều không có được hạnh phúc trọn vẹn. Tạo dựng kết thúc như vậy, Nguyễn Du đã tôn trọng logic trong hiện thực và của tính cách nhân vật.
Câu 9: Những thành công của nghệ thuật xây dựng nhân vật
Lời giải chi tiết:
Nguyễn Du gần như vẫn giữ nguyên hệ thống nhân vật trong tác phẩm Kim Vân Kiều truyện. Song tính cách của hầu hết những nhân vật đều được làm khác đi, phù hợp với chủ đề mới, phù hợp với bản sắc văn hóa và tâm hồn dân tộc.
Sự biến đổi của các nhân vật trung tâm tất nhiên dẫn đến sự đổi thay của tất cả nhân vật khác: Thúy Vân, Kim Trọng, Thúc Sinh, Hoạn Thư,... Họ đều xuất hiện trong tác phẩm của Nguyễn Du với những diện mạo vô cùng mới lạ, tính cách cũng mới lạ. Trong Kim Vân Kiều truyện, các nhân vật ấy ít có đời sống nội tâm và gần như không có bất cứ bi kịch nào nhưng ở Truyện Kiều, mỗi người đều mang một nỗi đau riêng
Những nhân vật trong Truyện Kiều đều được khắc họa một cách chân thực và sinh động, từ ngoại hình, cử chỉ, lời nói, hành động,... tới diễn biến nội tâm, Nguyễn Du đã cá thể hoá ngoại hình của các nhân vật sử dụng vô cùng thành công các chi tiết bề ngoài nhằm khắc họa tính cách (Thuý Vân, Thuý Kiều, Tú Bà, Mã Giám Sinh,...). Nhiều nhân vật trong tác phẩm Truyện Kiều có giọng điệu cùng vốn ngôn ngữ riêng, phản ánh rất chân thực nguồn gốc, lai lịch cùng như tính cách và diễn biến tâm trạng. Nhiều đoạn ngôn ngữ đối thoại có thể bộc lộ những biến động vô cùng tinh tế và phức tạp trong tâm hồn nhân vật.
Câu 10: Khám phá về thế giới nội tâm của nhân vật.
Lời giải chi tiết:
Thế giới nội tâm nhân vật đã được Nguyễn Du khám phá, thể hiện thông qua nhiều phương tiện cử chỉ, hành động cùng với ngôn ngữ đối thoại và độc thoại, lời nửa trực tiếp, "ngôn ngữ" thiên nhiên trong ấy, hình tượng thiên nhiên đã chiếm giữ vị trí rất quan trọng. Trong “Truyện Kiều” của tác giả Nguyễn Du, tác giả đã tập trung ngòi bút của mình cho nhân vật chính là Thuý Kiều nhằm việc thể hiện tình cảm nhân đạo cao cả của ông đối với nhân vật nàng Kiều. Ngoài nhân vật chính, ông đã xây dựng được hàng loạt những nhân vật có cá tính và đã trở thành nhân vật điển hình trong nền văn học: Kim Trọng, Hoạn Thư, Từ Hải, Tú Bà, Thúc Sinh, Mã Giám Sinh,… Ngay cả những nhân vật phụ tưởng như chỉ được nêu ra trong một vài câu thơ, Nguyễn Du cũng để lại cho độc giả những hình ảnh khó quên thông qua những màn và những cuộc hội thoại của Tác phẩm. Chúng ta có thể tìm thấy trong Tác phẩm của Nguyễn Du rất nhiều những hình thức hội thoại: đơn thoại, tam thoại, song thoại, đa thoại hay đối thoại giữa người âm với người dương, đối thoại trực diện cùng với đối thoại gián tiếp…
Có thể nói, bằng cách sử dụng những ngôn ngữ nửa trực tiếp trong đoạn độc thoại nội tâm của nhân vật, tác giả như muốn được hòa mình vào đó để tự do bày tỏ quan niệm, suy nghĩ và cách đánh giá của bản thân một cách khách quan. Nội dung và ngữ điệu hoàn toàn thuộc về nhân vật, nhưng chủ thể lời nói lại của người kể.
Một trong những nghệ thuật rất đặc sắc được tác giả Nguyễn Du đã thể hiện trong “Truyện Kiều” là hình thức hoạt động giao tiếp ngôn ngữ của mọi nhân vật trong truyện. Trong đó, độc thoại nội tâm chính là hình thức hoạt động rất đặc biệt của ngôn ngữ. Độc thoại nội tâm làm cho diện mạo tinh thần của tất cả nhân vật trở nên sắc nét, nổi bật và diện mạo, cảm quan của tác giả cũng được thể hiện một cách sinh động, độc đáo và sâu sắc. Đây cũng là điều mà các nhà nghiên cứu đã từng xác nhận được. Trong “Truyện Kiều” đó xuất hiện lời độc thoại nội tâm với những đặc trưng của nó là lời trực tiếp tự do, sử dụng ý thức và lời nửa trực tiếp trong tâm trạng của nhân vật.
Câu 11: Ngôn ngữ cùng với thể thơ lục bát
Lời giải chi tiết:
Thể thơ lục bát có trong ca dao, tức là đã xuất hiện từ rất lâu trước đấy, song lại chỉ trở nên hoàn mỹ khi có truyện Kiều. Truyện Kiều đã đưa được thể thơ lục bát lên một tầm cao mới, với đầy đủ những tính chất nghệ thuật, cái đẹp thiên cổ nhưng vẫn luôn giữ được nét giản dị của nó. Sử dụng thể thơ lục bát nhằm sáng tác tác phẩm, Nguyễn Du đã góp phần phát triển thêm tiếng Việt, ở thời kỳ ấy là chữ Nôm, không phải phụ thuộc vào dòng chữ hán của Trung Quốc, tìm cho mình một lối đi riêng nhưng mang đậm bản sắc dân tộc.
Tiếng Việt trong tác phẩm Truyện Kiều của nhà văn Nguyễn Du đã tạo ra một thế giới “chữ nghĩa”, “thế giới nghệ thuật” vô cùng độc đáo. Nhà văn sở hữu một “kho báu” từ vựng dồi dào, phong phú và đa dạng, xứng đáng là những khối cẩm thạch xây được tòa lâu đài chữ nghĩa Truyện Kiều. Điều ấy đã khẳng định về nghệ thuật ngôn từ của tác phẩm truyện Kiều. Trước hết, Nguyễn Du muốn tôn vinh cái giản dị nhưng chân thành trong tiếng Việt. Nhà thơ sử dụng nhiều từ ngữ dễ hiểu nhất và gần gũi với đời sống của nhân dân nhất để viết nên những trang thơ cho mình. Ông đề cao ngôn từ của những người dân lao động, mà vẫn tô điểm cho chúng những nét nghệ thuật rất đặc sắc. Với Truyện Kiều, thế giới biết hơn về một nước Việt Nam nhân văn, biết hơn về thứ Tiếng Việt lung linh, giàu sắc điệu và có thể diễn tả đầy đủ cung bậc tình người và khả năng thu nhận hay thuần hóa những thứ tiếng khác để tự làm giàu cho bản thân. Nguyễn Du là người vô cùng mạnh bạo và thành công nhất trong quá trình mở cửa cho những ngôn ngữ bình dân bước vào, không chỉ bước vào mà còn có thể làm chủ lâu đài văn học trước đây vốn chỉ chứa ngôn ngữ kinh sách, đầy tính tượng trưng và ước lệ. Nguyễn Du sử dụng tiếng Việt hết sức sáng tạo, Nguyễn Du là một nhà “thuần hóa” điển cố, thuần hóa được chữ Hán một cách thiên tài. Ông đã khiến cho tiếng Việt có khả năng không chỉ đạt được độ hàm súc ngang với chữ Hán mà còn thể hiện sự biểu cảm cao hơn, ít nhất là trong cảm thụ của người Việt Nam. Nguyễn Du lựa chọn những từ đã từng được Việt hóa và tiếp tục sáng tạo thêm ngôn ngữ bình dân gần lời ăn tiếng nói trong quá trình giao tiếp hàng ngày. Vì vậy, những từ: Hoa, Xuân, Thu, cúc, tâm, lan, tài, mệnh, đàn bà... đã đi vào đời sống một cách tự nhiên và dễ được tiếp nhận. Nhà thơ vẫn giữ những nét điển tích, điển cố trong tác phẩm, song không gây khó hiểu cho độc giả. Ngôn từ vô cùng bình dân chính là nét đẹp nhất trong tác phẩm truyện Kiều.
2.3 Trả lời câu hỏi sau khi đọc văn bản
Câu 1 trang 13 SGK Văn 11/2 Kết nối tri thức
Lập niêu biểu của nhà văn Nguyễn Du sau đó nêu nhận xét về cuộc đời và con người ông.
Lời giải chi tiết:
- Nguyễn Du sinh vào năm 1765 tại Thăng Long, tên chữ là Tố Như, lấy hiệu là Thanh Hiên.
- Năm lên 10, Nguyễn Du bị mồ côi cha.
- Năm 13 tuổi, lại mồ côi mẹ, Nguyễn Du tới sống với người anh cùng cha khác mẹ tên là Nguyễn Khản.
- Trong quãng thời gian này, ông đã có dịp hiểu biết thêm về cuộc sống phong lưu và xa hoa của giới quý tộc phong kiến - những điều ấy đã để lại dấu ấn trong những sáng tác của ông sau này.
- Năm 1783, Nguyễn Du thi Hương đỗ tam trường (tú tài) sau đó được tập ấm nhận một chức quan vő nho nhỏ ở Thái Nguyên.
- Từ năm 1789 - 1796, Nguyễn Du phiêu bạt trên đất Bắc sau đó về ở ẩn tại quê nội thuộc tỉnh Hà Tĩnh từ năm 1796 - 1802.
- Năm 1802, Nguyễn Du được làm quan cho nhà Nguyễn và nhậm chức Tri huyện Phù Dung (nay thuộc Khoái Châu, tỉnh Hưng Yên), sau đổi thành Tri phủ Thường Tín (nay thuộc địa phận Hà Nội).
- Từ năm 1805 - 1809, ông tiếp tục được thăng chức Đông Các điện học sĩ.
- Năm 1809, Nguyễn Du được bổ nhiệm làm Cai bạ dinh Quảng Bình.
- Năm 1813, ông được thăng lên làm Cần Chánh điện học sinh và giữ chức Chánh xứ và đi Trung Quốc.
- Đến khi qua Trung Quốc, Nguyễn Du được tiếp xúc gần gũi với nền văn hóa mà từ nhỏ đã quen thuộc.
- Năm 1820, Nguyễn Du được cử đi làm Chánh sứ tại Trung Quốc, nhưng chưa kịp lên đường đã mất mạng vào ngày 10 tháng 8 năm 1820.
- Năm 1965, Hội đồng Hòa bình thế giới đã công nhận đại thi hào Nguyễn Du là Danh nhân văn hóa thế giới.
=> Nhận xét: Cuộc đời của Nguyễn Du đã trải qua vô vàn biến cố gắn với bối cảnh của thời đại. Nguyễn Du là một người có kiến thức sâu rộng, am hiểu về văn hóa dân tộc và văn chương của Trung Quốc.
Câu 2 trang 13 SGK Văn 11/2 Kết nối tri thức
Bắc hành tạp lục được sáng tác vào hoàn cảnh như thế nào? Nội dung chính trong tập thơ ấy là gì?
Lời giải chi tiết:
- Bắc hành tạp lục đã được sáng tác vào thời gian Nguyễn Du đi sứ Trung Quốc.
- Nội dung chính: Niềm cảm thương và trăn trở đến day dứt trước số phận của con người, đặc biệt là thân phận của những con người tài hoa.
Câu 3 trang 13 SGK Văn 11/2 Kết nối tri thức
Nêu lên những giá trị cơ bản trong thơ chữ Hán Nguyễn Du.
Lời giải chi tiết:
- Thơ chữ Hán của tác giả Nguyễn Du vừa lưu giữ thế giới tâm hồn vô cùng phong phú và phức tạp của một nghệ sĩ lớn, lại vừa có khả năng khái quát về hiện thực rất cao và mang tới giá trị nhân văn vô cùng sâu sắc.
- Ba tập thơ còn phản chiếu lên chân dung của con người và sự vận động tư tưởng nghệ thuật của tác giả. Đó là hành trình đi từ hiểu chính mình, thương mình tới thấu hiểu con người và thương người.
Câu 4 trang 13 SGK Văn 11/2 Kết nối tri thức
Tóm tắt lại cốt truyện Truyện Kiều ( dài khoảng 1 - 1,5 trang)
Lời giải chi tiết:
- Phần 1: Gặp gỡ và đính ước
Truyện Kiều được kể về cuộc đời của nhân vật Thúy Kiều - một thiếu nữ có tài sắc vẹn toàn nhưng cuộc đời lại chứa đầy những bất hạnh. Trong một lần đi du xuân, Kiều vô tình gặp được Kim Trọng và có một mối tình hết sức đẹp đẽ bên chàng Kim. Hai người chủ động gặp gỡ sau đó đính ước với nhau.
- Phần 2. Gia biến và lưu lạc
Gia đình Kiều bị nghi oan, cha nàng bị bắt, Kiều quyết định phải bán mình đi để chuộc cha. Trước khi bán mình, Kiều đã trao duyên cho người em gái là Thúy Vân. Thúy Kiều bị bọn buôn người bao gồm Mã Giám Sinh và Tú Bà lừa bán vào trong lầu xanh. Sau đó, nàng được Thúc Sinh cứu vớt ra khỏi cuộc đời của kỹ nữ. Nhưng rồi Kiều lại bị Hoạn Thư - vợ của Thúc Sinh ghen tuông và đày đọa. Nàng một lần nữa lại rơi vào chốn thanh lâu. Ở đây, Kiều gặp được nhân vật Từ Hải - một người “anh hùng đầu đội trời, chân đạp đất”. Từ Hải lấy Kiều và sau đó giúp nàng báo ân báo oán. Vì mắc lừa tổng đốc Hồ Tôn Hiến, Kiều vô tình đã đẩy Từ Hải vào đường chết. Đau đớn, nàng reo mình xuống sông thì được sư Giác Duyên cứu sống.

- Phần 3. Đoàn tụ
Lại nói tới Kim Trọng khi từ Liêu Dương chịu tang chú quay trở về, biết Thúy Kiều gặp phải biến cố thì hết sức đau lòng. Chàng kết hôn với Thúy Vân nhưng vẫn ngày nhớ đêm mong gặp lại nàng Kiều. Chàng liền quyết tâm phải đi tìm nàng để gia đình đoàn tụ. Thúy Kiều nối lại duyên xưa với Kim Trọng nhưng cả hai đã cùng nguyện ước “duyên đôi lứa cũng là duyên bạn bầy”.
Câu 5 trang 13 SGK Văn 11/2 Kết nối tri thức
Văn bản đã phân tích về những nội dung cơ bản gì trong tư tưởng nhân đạo của Truyện Kiều?
Lời giải chi tiết:
- Tôn vinh lên vẻ đẹp của con người, đặc biệt là người phụ nữ.
- Đồng cảm và đồng tình trước những khát vọng chính đáng và dám vượt ra ngoài những khuôn phép phản nhân văn của tư tưởng thời phong kiến.
Câu 6 trang 13 SGK Văn 11/2 Kết nối tri thức
Nguyễn Du đã có những sáng tạo như thế nào trên bình diện tổ chức cốt truyện và xây dựng những nhân vật trong tác phẩm Truyện Kiều?
Lời giải chi tiết:
Cốt truyện của Truyện Kiều được mượn từ tiểu thuyết Kim Vân Kiều truyện và vì thế phải chịu ảnh hưởng trực tiếp từ những nghệ thuật dựng truyện trong tiểu thuyết cổ điển Trung Quốc.
Về nghệ thuật xây dựng các tuyến nhân vật, Nguyễn Du đã có những sáng tạo như sau:
- Để điển hình hóa nhân vật, Nguyễn Du đã sắp xếp những chi tiết miêu tả ngoại hình nhân vật trong Kim Vân Kiều Truyện vào phần giới thiệu ngay đầu, đồng thời cũng điểm tô và chăm chút bằng những nét mới lạ.
- Đó mới chỉ là bước miêu tả chân dung bên ngoài, điều khiến cho sự trường tồn của tác phẩm Truyện Kiều chính là thế giới nội tâm hết sức phong phú, tinh tế và sâu sắc của nhân vật, khiến cho mỗi nhân vật có một đời sống riêng biệt, một sức sống khác nhau, lay động được lòng người, đi vào và sống giữa nhân gian như những con người thực sự. Đây cũng thể hiện lên trái tim yêu thương trong con người vô bờ bến của Nguyễn Du. Vì yêu thương nên cũng nhân lên vẻ đẹp cao quý trong tâm hồn và thông cảm sâu sắc với nỗi đau từ tận đáy của con người, tập trung cao độ vẫn là ở nỗi đau khổ của nhân vật nàng Kiều.
- Một biệt tài khác của tác giả Nguyễn Du chính là tả cảnh ngụ tình. Do tính chất của truyện là kể bằng văn, tác giả Thanh Tâm Tài Nhân không dành quá nhiều những câu tả cảnh ngụ tình. Tiêu biểu là trong đoạn Kiều ở lầu Ngưng Bích. Kim Vân Kiều Truyện đã miêu tả: “Thúy Kiều đề xong (thơ), thì lòng ngao ngán, con mắt đăm đăm trông ra bên ngoài, thấy những cỏ hoa mơn man, non nước mông mênh, gió cuốn mặt ghềnh, sóng dồn cửa bể, trông xa xa lại những con thuyền xuôi ngược, cánh buồm phất phơ.”
Câu 7 trang 13 SGK Văn 11/2 Kết nối tri thức
Dựa vào văn bản, hãy xác định những đóng góp quan trọng của tác giả Nguyễn Du đối với nền văn học của dân tộc.
Lời giải chi tiết:
Nguyễn Du đã để lại cho người đời cả một kho tàng văn học và văn chương bất hủ, phong phú với khoảng hơn một ngàn tác phẩm bao gồm cả tác phẩm chữ hán và chữ nôm. Ở lĩnh vực nào, Nguyễn Du cũng đều đạt được nhiều thành tựu xuất sắc và làm nổi bật đến trình độ cổ điển.
Trong đấy, sáng tác chữ Hán gồm: Thanh Hiên thi tập (bao gồm 78 bài), viết chủ yếu vào những năm tháng trước khi ông làm quan nhà Nguyễn; Nam trung tạp ngâm (bao gồm 40 bài thơ), làm từ năm 1805 tới cuối năm 1812, ông viết khi đã làm quan ở Huế, Quảng Bình và những địa phương nằm ở phía nam tỉnh Hà Tĩnh; Bắc hành tạp lục (được Ghi chép trong chuyến đi sang phương Bắc, bao gồm 131 bài thơ), viết trong chuyến đi sứ qua Trung Quốc. Sáng tác chữ Nôm, bao gồm: Đoạn trường tân thanh (tức Tiếng kêu mới về nỗi đau tới đứt ruột), hay Truyện Kiều, gồm 3254 câu thơ viết theo thể lục bát; văn chiêu hồn (nguyên là Văn tế thập loại chúng sinh, có nghĩa là Văn tế mười loại người), là một ngâm khúc bao gồm 184 câu viết bằng thể thơ song thất lục bát; thác lời trai phường nón (bao gồm 48 câu), cũng được viết bằng thể thơ lục bát, nội dung thay lời người con trai phường nón làm thơ để tỏ tình với một cô gái phường vải; văn tế sống Trường Lưu nhị nữ bao gồm 98 câu, viết dựa trên lối văn tế…
Nguyễn Du nổi bật giữa bầu trời văn chương tựa như một vì sao rực rỡ. Ông đã đem tới cho nền văn học vào thế kỉ XVIII và nền văn học của dân tộc những tiếng nói chan chứa tình người, được bao bọc bởi những hình thức nghệ thuật tuyệt đẹp chưa từng có. Ông luôn đề cao mặt xúc cảm và dạt dào tình người. Nét nổi bật nhất chính là sự cảm thông sâu sắc của ông đối với cuộc sống và với con người, đặc biệt là những con người vốn nhỏ bé và bất hạnh. Ông tập trung vào thể hiện sự trân trọng và đề cao giá trị con người trong chính cuộc sống của họ. Cái nhìn vô cùng nhân đạo ấy khiến cho ông được đánh giá là một nhà nhân đạo xuất sắc trong thế kỉ 18, 19 và trong nền văn học dân tộc. Hơn nữa, Nguyễn Du tỏ ra uyên bác và thâm thúy với cả những thể loại thơ cổ của Trung Quốc lẫn thơ của dân tộc. Thơ Nguyễn Du luôn nhịp nhàng mang tới âm thanh, bừng lên màu sắc của sự sống, hằn lên những đường nét rất sắc cạnh của bức tranh hiện thực vốn đa dạng.
Với những đóng góp nêu trên, Nguyễn Du xứng đáng được mệnh danh là Đại Thi Hào của dân tộc. Sáng tác của Nguyễn Du không quá đồ sộ về số lượng, nhưng nó đã kết tinh được văn học và văn hóa của dân tộc để trở thành đỉnh cao trong văn học của dân tộc nói riêng và nhân loại nói chung.
3. Kết nối đọc -viết trang 13 SGK Văn 11/2 Kết nối tri thức
Viết một đoạn văn (dài khoảng 150 chữ) phân tích một biểu hiện tư tưởng nhân đạo trong tác phẩm Truyện Kiều
Lời giải chi tiết:
Giá trị nhân đạo là một điều mà ta có thể dễ dàng bắt gặp ở tác phẩm Truyện Kiều. Trong đó, ấn tượng nhất đối với em chính là giá trị phê phán của tác phẩm. Mỗi con người, nhân vật trong tác phẩm Truyện Kiều của tác giả Nguyễn Du đều mang những mặt xấu và mặt tốt lẫn lộn đan xen. Từ kẻ buôn người như Tú Bà hay Bạc Bà cho tới kẻ độc ác như Hoạn Thư… tất cả đều mang theo mình những mặt đáng chê trách và lên án. Với Nguyễn Du, ông phê phán họ là thế, nhưng ông vẫn bộc lộ lòng khoan dung và sự tin tưởng của bản thân vào nhân cách của con người có thể được cảm hóa thể hiện thông qua đoạn Thúy Kiều báo ân báo oán. Và đó cũng chính là một phát hiện rất vĩ đại và to lớn khi ông luôn tin vào nhân phẩm của mọi người, họ chỉ là có lúc lầm đường lạc lối nhưng khi đã được khai sáng, họ sẽ quay lại với bản chất vốn có của mình và lại làm người lương thiện. Đây chính là giá trị nhân đạo mà em cảm thấy hay và sâu sắc nhất trong kiệt tác Truyện Kiều.
Đại thi hào Nguyễn Du đã góp phần đưa văn học Việt Nam trở thành một phần trong tinh hoa văn hóa toàn nhân loại. Ngoài việc có thêm thông tin, soạn bài Nguyễn Du – Cuộc đời và sự nghiệp còn giúp các em có những lối mở bài, kết bài và liên hệ hấp dẫn. Hy vọng sau khi tham khảo bài viết, các em có thể ghi nhớ những thông tin quan trọng. Ngoài ra, để học thêm những học phần khác thuộc chương trình ngữ văn 11 hoặc tất cả các môn học khác, các em nhanh tay truy cập vào website vuihoc.vn hoặc đăng ký những khoá học của VUIHOC để trải nghiệm học cùng các thầy cô ngay nhé!
Nguồn:





















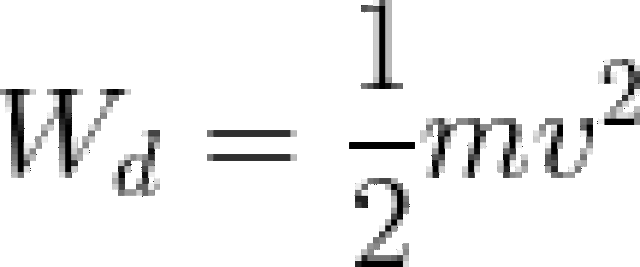
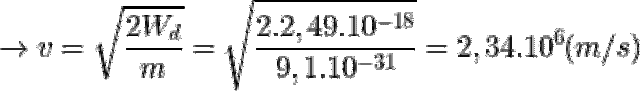

 nên lực Lorenxơ là lực hướng tâm, do đó ta có:
nên lực Lorenxơ là lực hướng tâm, do đó ta có: 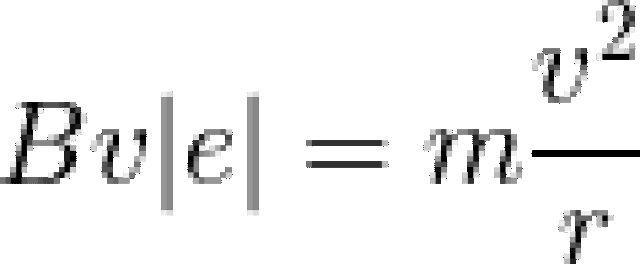
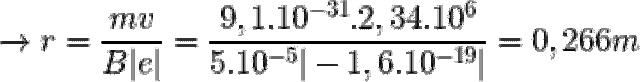
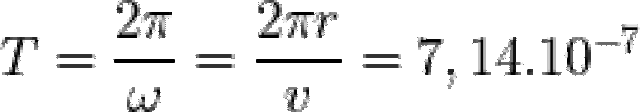
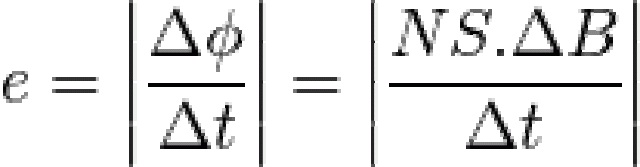
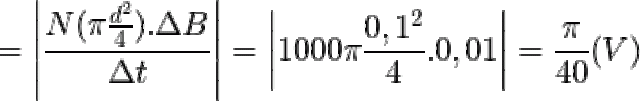
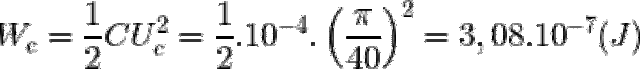
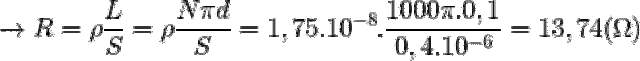
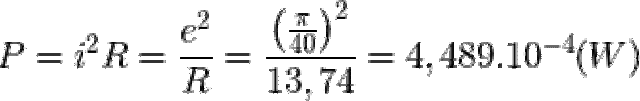








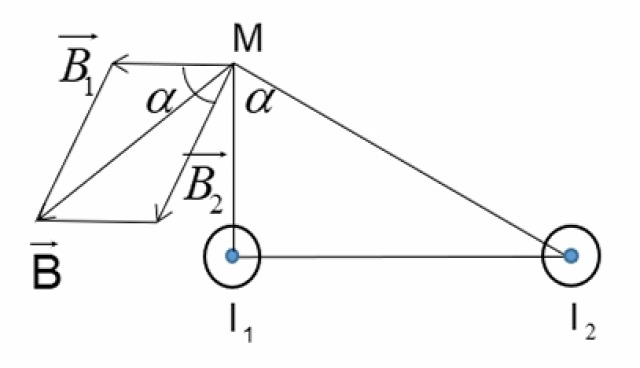
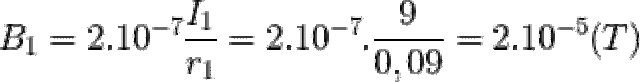
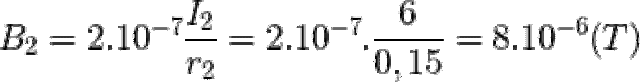
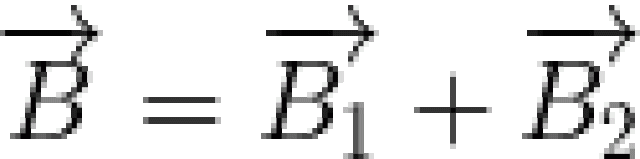
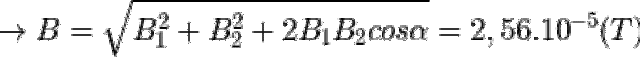
 = N.B.S.cos
= N.B.S.cos ; N = 150 vòng ; B = 0,6T
; N = 150 vòng ; B = 0,6T = 60o
= 60o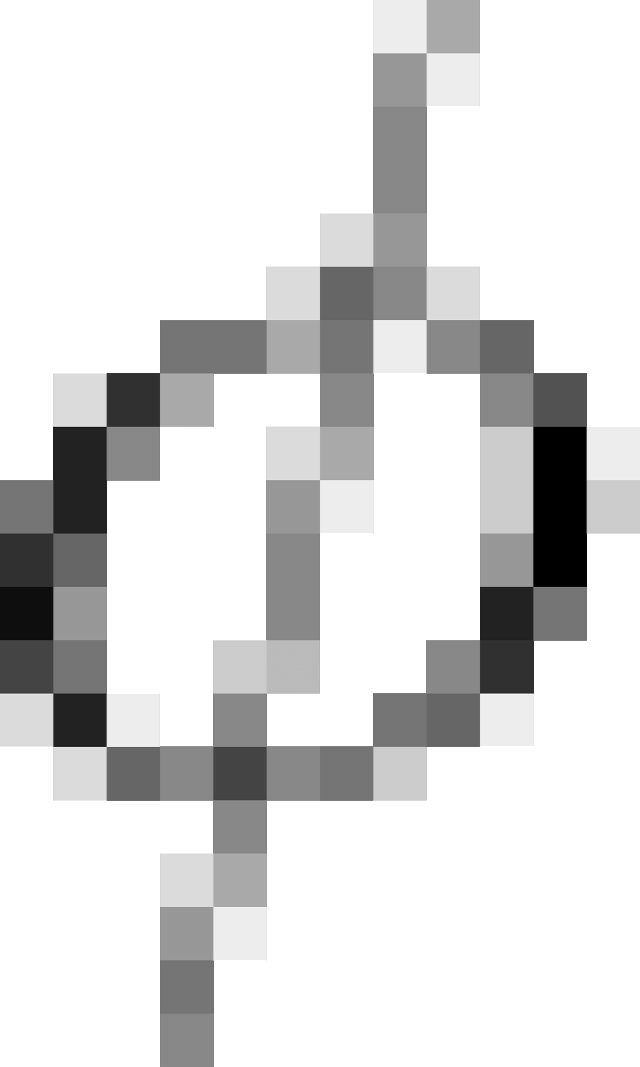 = 150.0,6.0,02.cos60o = 0,9 Wb
= 150.0,6.0,02.cos60o = 0,9 Wb  B = 1,5 - 0,6 = 0,9T
B = 1,5 - 0,6 = 0,9T
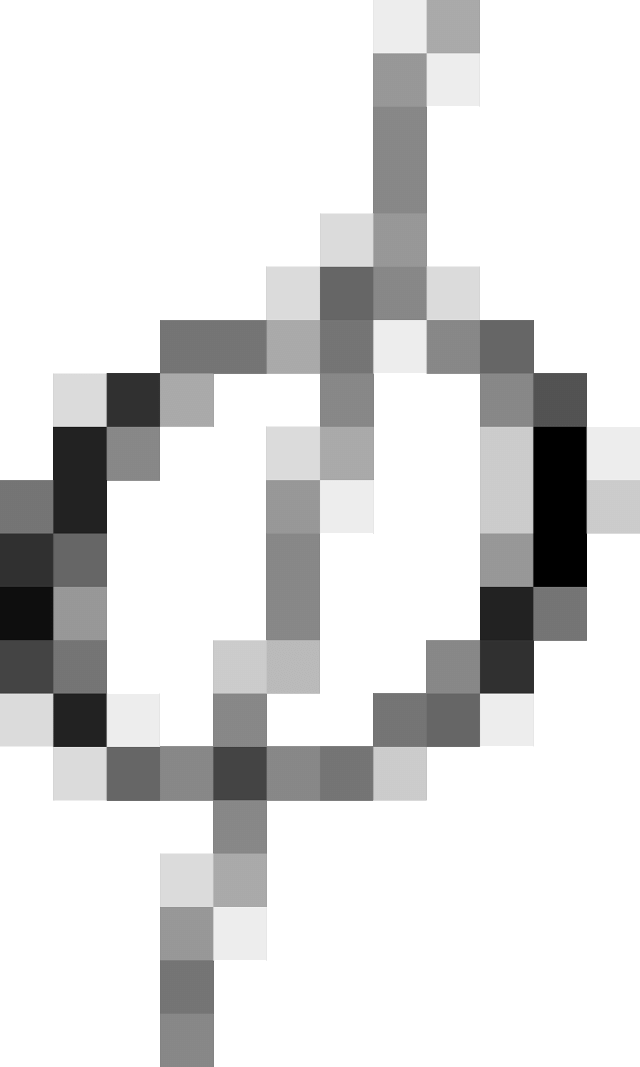 = 150.0,9.0,02.cos60o = 1,35 Wb
= 150.0,9.0,02.cos60o = 1,35 Wb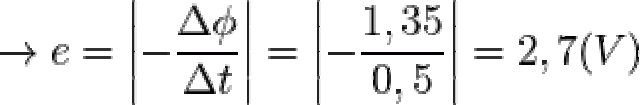



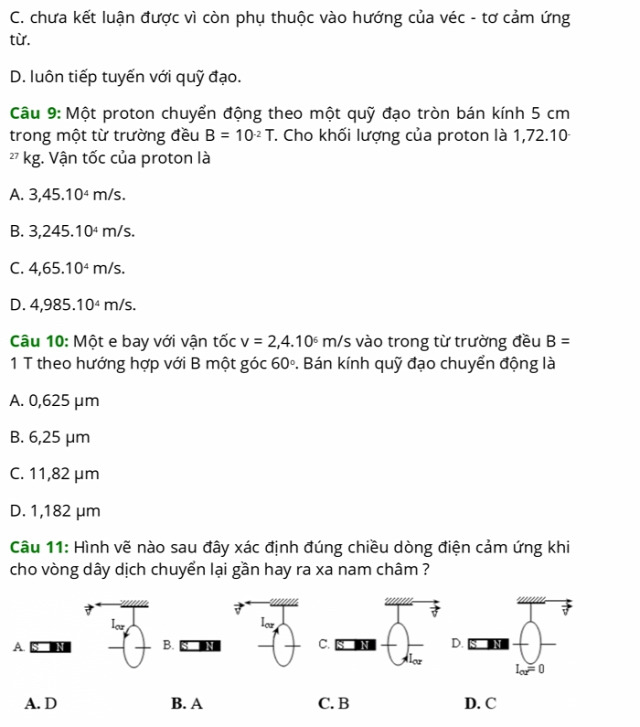





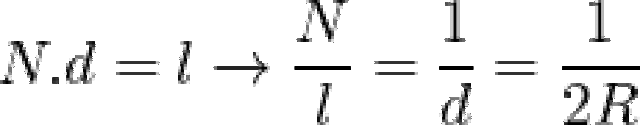
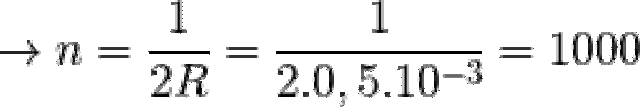 (vòng/m)
(vòng/m)